Aufgabe A 2.1
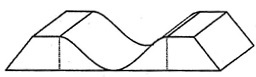Die nebenstehende Abbildung zeigt eine Station in einem Bikepark, die aus zwei seitlichen Wällen
und einer Fahrrinne besteht.
Die Abbildung in der Anlage zeigt modellhaft ihren Querschnitt.
Dabei wird die Fahrrinne durch den Graphen einer Funktion f im Bereich -8≤x≤8 modelliert
(Angaben in Meter).
Die Querschnitte der Wälle sind grau markiert.
Der horizontale Untergrund wird im Querschnitt durch die x-Achse beschrieben.
Die Station hat auf der gesamten Länge den in der Abbildung gezeigten Querschnitt.
Abbildung zu Aufgabe A 2.1
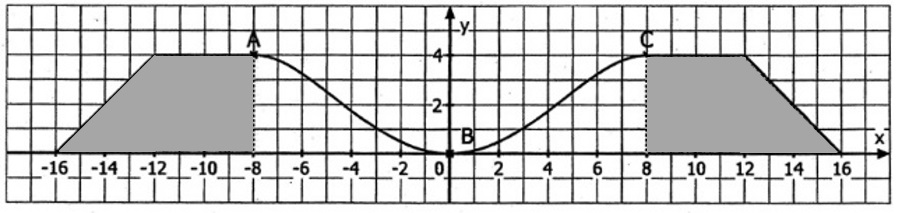
Bestimmen Sie die Breite der Fahrrinne in einer Höhe von 1 m über dem Untergrund.
Ermitteln Sie die mittlere Steigung zwischen den im Modell mit B und C bezeichneten Punkten.
Bestimmen Sie die maximale Steigung der Fahrrinne.
Begründen Sie, dass f keine ganzrationale Funktion zweiten Grades sein kann.
(4,5 VP)
b) Es ist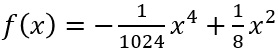
.Berechnen Sie die Höhe, in der die Fahrrinne eine Breite von 12 m hat.
Das verbaute Material hat ein Gesamtvolumen von 1168 m³.
Ermitteln Sie die Länge der Station.
(5 VP)
c) Die abgebildete Fahrrinne lässt sich auch näherungsweise durch den Graphen einer trigonometrischen Funktion g modellieren, der die Punkte A, B und C als Extrempunkte besitzt.Bestimmen Sie einen möglichen Funktionsterm von g.
(2,5 VP)
Aufgabe A 2.2
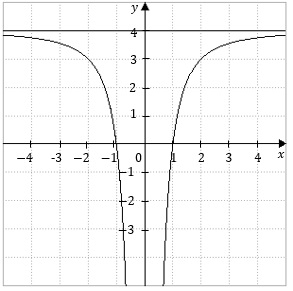
Gegeben ist die Funktion f durch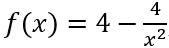 
; x≠0.Ihr Graph K sowie die Gerade g: y=4 sind in der nebenstehenden Abbildung dargestellt.
a) Der Punkt P(u|v) mit u>0 ist ein Punkt auf g.
Die Punkte P, Q(u|4), R(0|4) und S(0|v) sind die Ecken eines Rechtecks.
Bei Rotation dieses Rechtecks um die y-Achse entsteht ein Zylinder.
Zeigen Sie, dass das Volumen dieses Zylinders unabhängig von u ist.
Berechnen Sie denjenigen Wert von u, für den der Inhalt der Mantelfläche des Zylinders
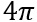beträgt.
(4 VP)
b) Für jeden Punkt auf K begrenzen die zugehörige Tangente an K, die Gerade g und die y-Achse ein Dreieck. Für einen solchen Punkt T mit positiver x-Koordinate ist dieses Dreieck gleichschenklig.Berechnen Sie die x-Koordinate dieses Punktes T.
(2 VP)
c) C ist der Graph der Funktion h mit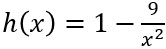
.K geht durch eine Streckung in y-Richtung und eine Streckung in x-Richtung aus C hervor.
Ermitteln Sie die beiden zugehörigen Streckfaktoren.
(2 VP)
| Downloads |
PowerPoint